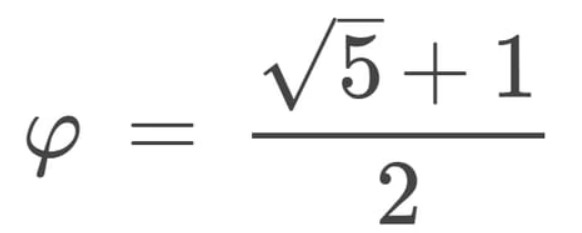Origine de Fibonacci
Leonardus Pisanus qui a pris le nom de Fibonacci, certainement par contraction de Filius Bonacii (le fils de Bonacii) est un mathématicien italien né en 1170 et décédé en 1250.
Il a participé à de nombreux travaux, mais il est plus connu pour sa suite, la suite de Fibonacci. Cette suite est formée de nombre entier, dont chacun est la somme des deux qui le précède :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, etc.
De manière scientifique, la suite s’écrit :
F(0) = 0, F(1) = 1 et F(n) = F(n-1) + F(n-2) pour n au moins ègale à 2
Avec n un Nombre entier.
À titre d’exemple, pour n=3 le résultat de la suite est :
F3 = F2 + F1 = F0 + F1 + F1 = 0 + 1 + 1
F3 = 2
Cette suite est importante, car lorsque l’on divise l’un des résultats de la suite par son précédent, on retombe toujours sur le nombre d’or découvert par Euclide. Ce nombre est très important, notamment en géométrie où il apparait fréquemment.
On note 𝛗, le nombre d’or égal à :
Ce dernier est égal à 1.618.
De même, si vous divisez un nombre par son suivant, alors vous obtiendrez 0.618.
C’est donc sur ce nombre d’or que les retracements de Fibonacci utilisés en trading sont basés.
